Semantic Program Embeddings

Role: Co-First Author

The goal of this project was to understand how to embed programs into vector spaces in a way that respects program semantics, as many machine learning techniques attempt to do. In most areas of machine learning (e.g., computer vision and natural language processing), researchers may claim an embedding technique “captures semantics”, and because there’s no formal way to ground the term “semantics”, it’s usually interpreted loosely. Programming languages are different; a programming language has a very precise notion of semantics. Our first insight was that because programming languages are formal objects, one can theoretically reason about semantic embeddings of them. There are many types of semantic properties one may wish to embed, and in our first preprint, we focused on formalizing the frequently cited desideratum that ``embeddings of similar programs are close’’ and developed a technique motivated by optimization for this property. Our technique embeds numerical programs using orthogonal polynomials and produces embeddings that preserve distances more effectively than a BERT-Tiny.

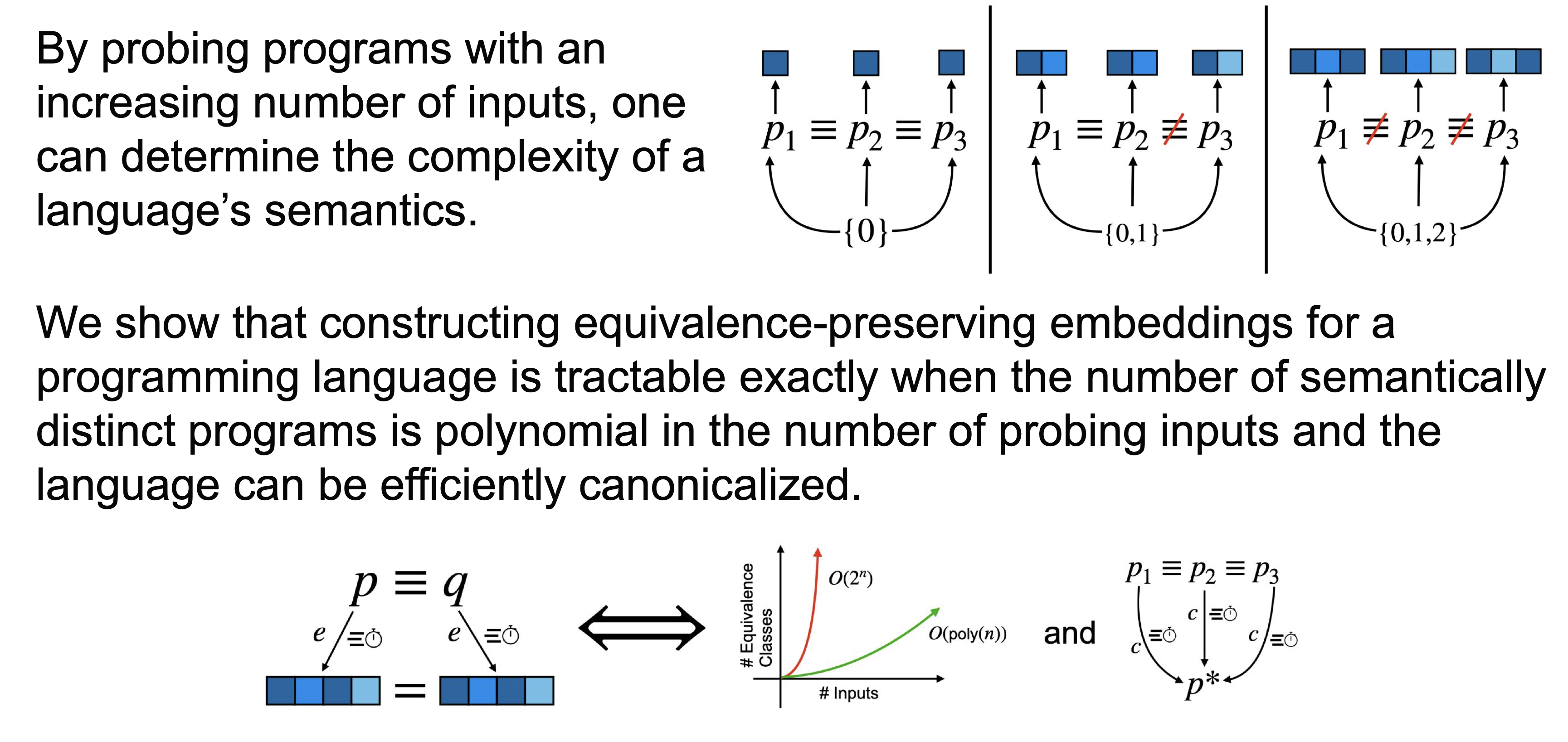
Since there is not a canonical notion of distance between non-numerical programs, we sought a more fundamental property than distance preservation. At the time of this work, there was a push for code models that were adversarially robust, often implemented by training for embeddings that are invariant to semantics-preserving transformations. The implication of this invariance is that the embedding preserves semantic equivalences, and in our second preprint, we theoretically characterized the computational complexity of producing such embeddings. The core insights that came from this study were (1) that a programming language must have finitely many semantic equivalence classes for such an embedding function to exist and (2) that such an embedding function exists iff your programming language has an efficient canonicalizer. The theory isn’t deep here, and with our definitions in place, these insights are trivial. The contribution here was a lucid set of definitions rather than a theory of great technical complexity.

µTVM

Role: First Author

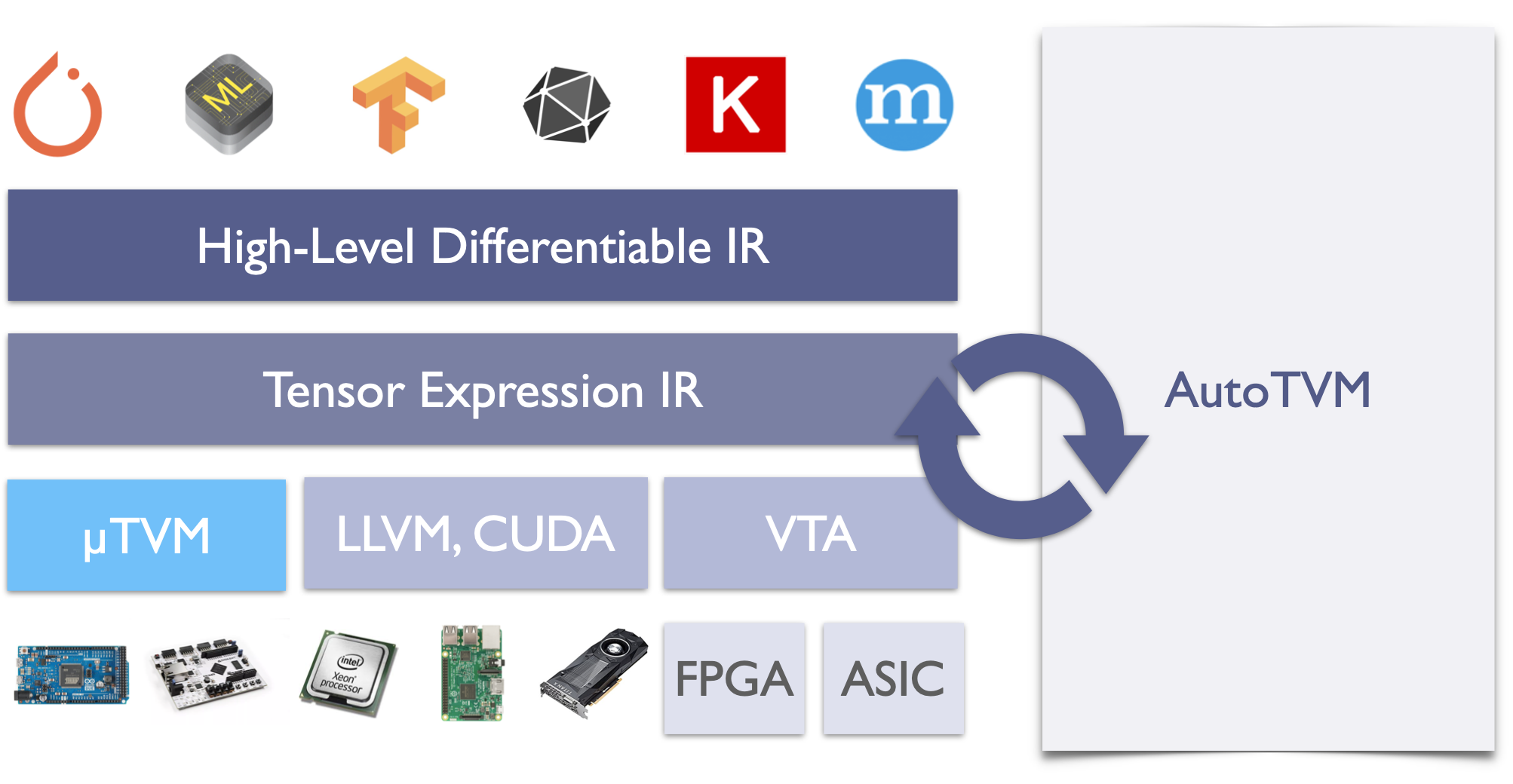
µTVM brings the power of Apache TVM to bare-metal devices. Using a lightweight and device-agnostic runtime for interacting with microcontrollers, µTVM plugs directly into the TVM stack and provides automatic optimization of ML operators. The figure below gives an idea of where µTVM sits in TVM.

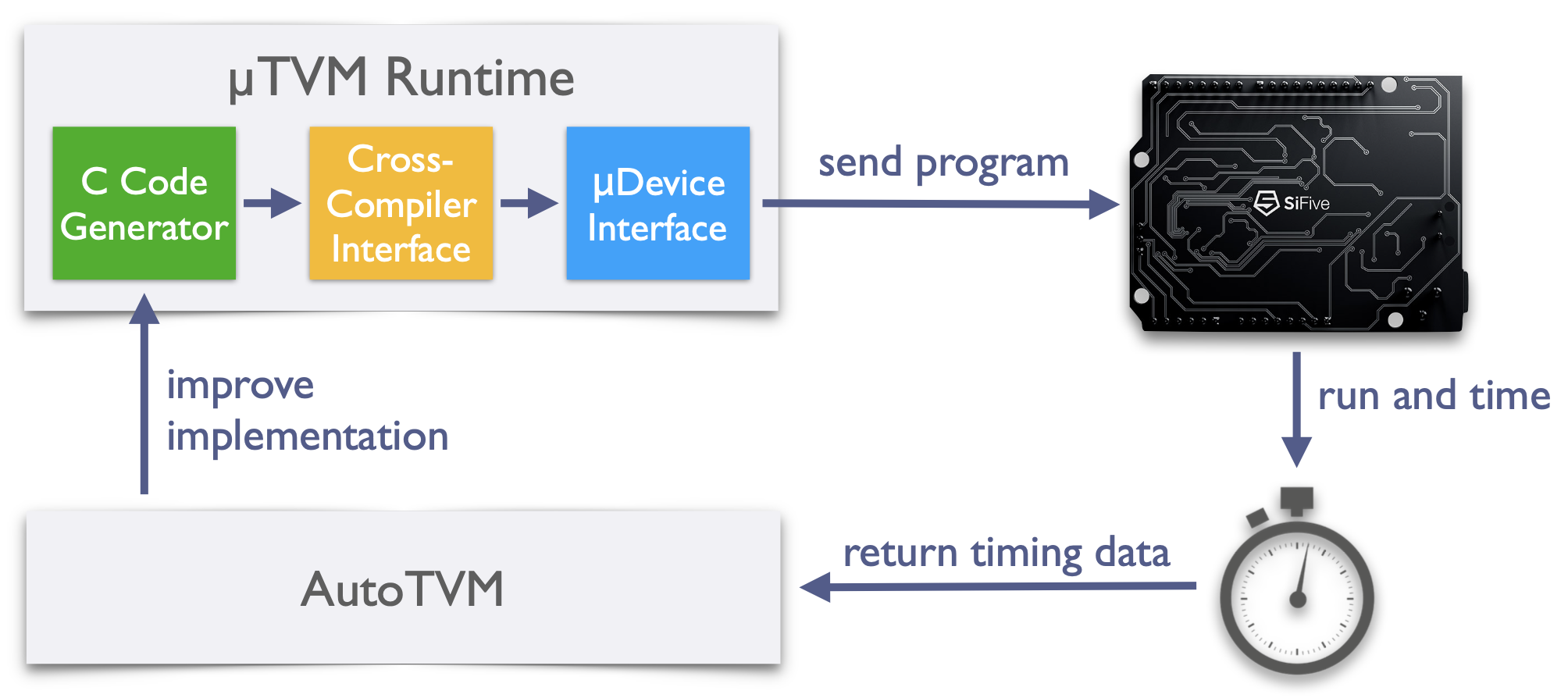
To provide automatic optimization, µTVM makes use of AutoTVM (depicted below). AutoTVM suggests candidate kernel implementations in C, which µTVM then compiles and loads onto the device via JTAG. Random inputs are used to time the execution of kernels, and these inputs are then fed into AutoTVM’s search algorithm. By intelligently navigating the space of implementations, AutoTVM tailors candidate kernels to the architectural properties of the device, using only timing information.

Relay

Role: Collaborator

Every time you ask Amazon Alexa a question, Relay is being used.

Relay is a functional and differentiable intermediate representation for machine learning applications, which ditches the design of traditional computation-graph-based IRs, and instead opts to be a full-fledged programming language. The design is surprisingly similar to the language SML, with the key difference being a tensor-based type system with a lightweight form of dependency.

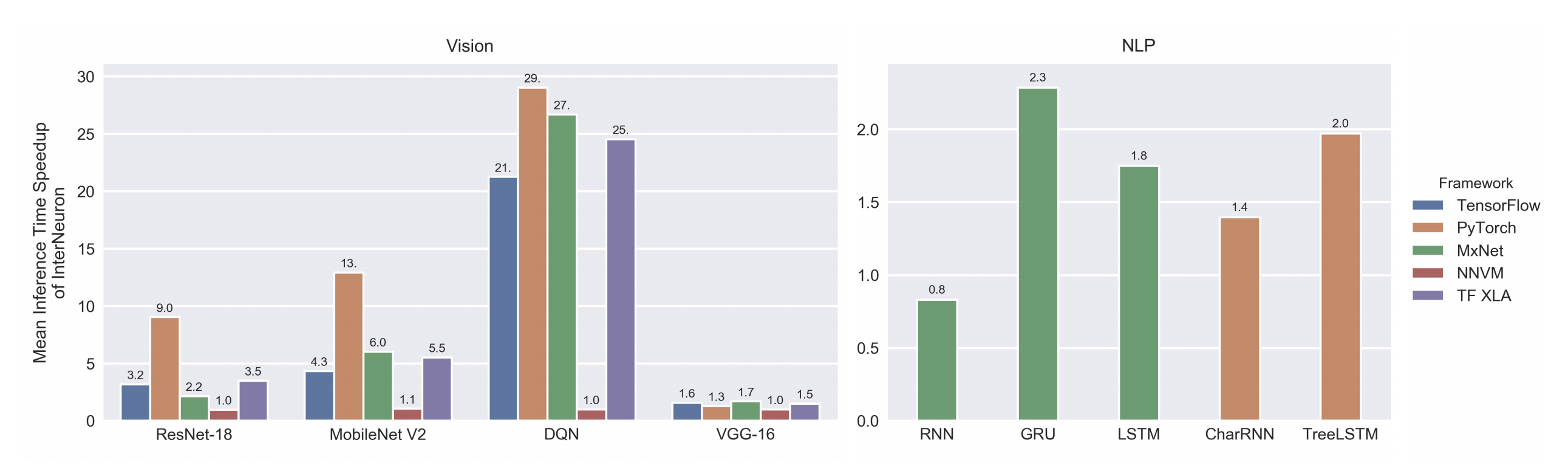
Relay is tightly integrated with Apache TVM and sits on top of TVM’s low-level tensor expression IR. This split creates a separation of concerns, where Relay orchestrates the high-level flow of models and calls into kernels that have been aggressively optimized in the low-level IR. By using a two-level IR split, Relay significantly outperforms existing machine learning frameworks (shown below).